소리(Sound)는 파동(Wave)이다. 물체가 진동(Vibration)하여 주변공기 입자를 진동시키면 진동이 공간으로 번져 나간다. 공간으로 전파하는 진동이 곧 파동으로서 매질인 공기입자는 그자리에서 진동만 할 뿐 이동하지는 않는다. 마치 잔잔한 호수에 돌을 던지면 물결파가 동심원을 그리며 번지는 것과 같다. 이때 물위에 낙엽이 하나 떠 있다면 물결파를 따라서 낙엽이 호숫가로 이동하지 않고 그자리에서 위 아래로 운동하게 된다. 낙엽은 물입자의 운동을 보여준다. 물결파와 같이 파동의 이동방향과 매질의 진동방향이 수직인 경우를 횡파(Shear wave)라 한다. 반면에 소리는 종파(Longitudinal wave)라고 부르는데 이는 소리가 진행하는 방향으로 공기가 진동한다는 의미가 된다. 이 때문에 문풍지나 풍선에 입을 대고 소리를 내면 문풍지나 풍선이 앞뒤로 떨리는 것이다.
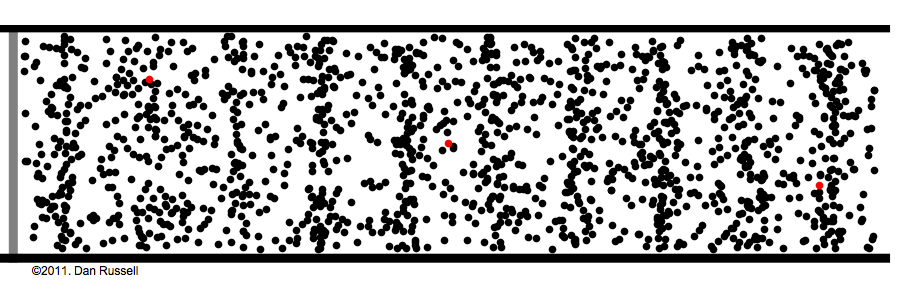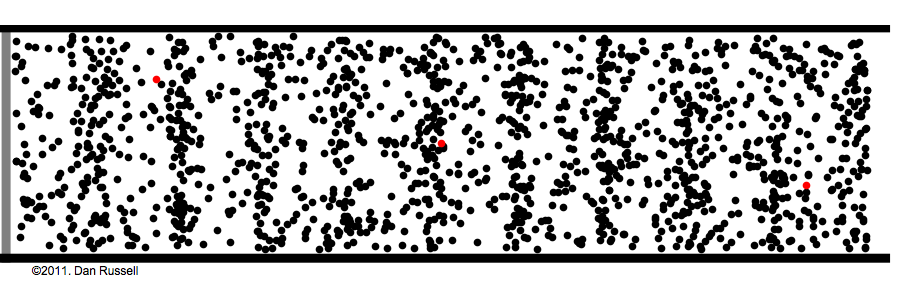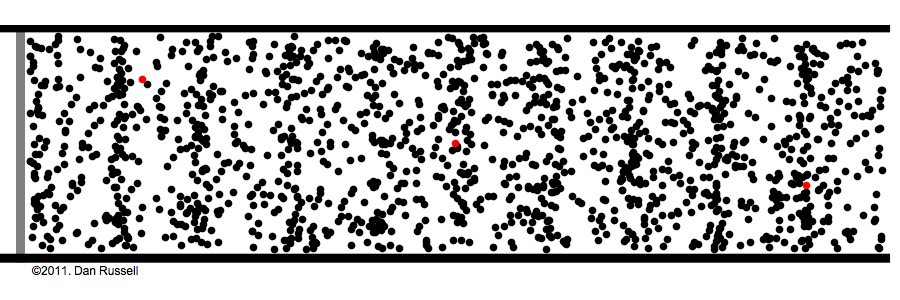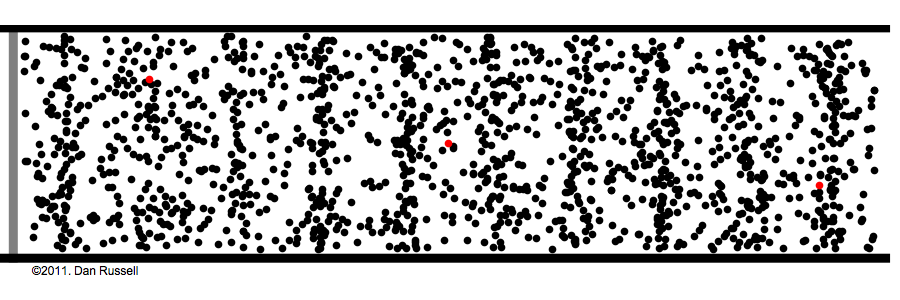
[그림1] 소리의 진행(왼쪽 피스톤과 빨간점을 유의해 보기 바람)
1) 파동을 나타내는 용어
파동을 이해할 경우는 물결파를 이용하면 이해하기가 쉽다. 물결파가 진행할 때 진행방향으로 칼로 물을 베듯이 단면을 만들어 옆으로 보면 물표면이 Sine 파형으로 되는 것을 알 수 있다. 이 단면을 그림으로 나타내면 오른쪽 그림이 된다. 이 경우는 마치 스냅사진을 찍어 공간적으로 파동을 표현한 것으로 볼 수 있다. 즉, 시간을 고정하고 공간적으로 파동을 표현한 것이다.
[그림 2] 물결파의 공간 표현
따라서 가로축은 공간좌표가 될 것이며, 세로축은 물표면의 위치변화(변위)를 나타낸다. 따라서 골과 골사이나 마루와 마루 사이 즉, 동일 위상 사이를 파장(波長=Wave length;
)이라 하며, 최대 변위를 진폭(Amplitude)이라고 한다.
파동을 표현하는 방법은 두가지가 있다. 위와같은 방법과 다음과 같이 수면위에 낙엽이 하나 있을 경우에 낙엽이 시간에 따라 위치변화(변위)하는 모습으로 표현하는 방법이다. 즉, 공간상에 한 점을 고정하고 그 지점에 있는 매질입자의 변위를 시간에 따라 표현하는 것이다. [그림 3]과 같이 가로축을 시간좌표로 놓는다. 이 경우는 가로축의 마루와 마루 사이 즉, 동위상 사이를 주기(Period; T)라 한다. 세로축이 진폭인 것은 위 방법과 동일하다.
주기란 한 파장의 파동이 만들어지는 시간으로서 진동수와 역수관계가 성립한다. 진동수는 1초에 한 지점을 지나가는 파장의 갯수이며 1초에 만들어지는 파동의 갯수임으로 이 성립한다. 따라서 주기를 알면 진동수를 구할 수 있다.
또, 파동의 전파속도는 1초에 진행하는 거리이므로 파동의 길이와 진동수(주파수)를 곱하여 구할 수 있다. 이는 사람의 걷는 속도를 보폭에 1초에 걷는 걸음수로 나타낼 수 있는 것과 같다. 그러므로 음속은 다음과 같다.
[그림 3] 시간축으로 표현한 위치변화
[그림 4]종파의 횡파적 표현(+변위: 진행방향 변위, -변위: 진행방향 반대 변위)
2) 종파의 횡파적 표현
물결파의 단면에서 보듯이 횡파는 Sine파형이 됨을 쉽게 이해 할 수 있으나 종파인 소리를 물결파와 같이 Sine파형으로 표현하는 것은 잘 이해가 되지 않는다. [그림 4]에서 보는 바와같이 그림에서 소리가 왼쪽에서 오른쪽으로 진행한다고 할 때 매질입자가 평형점에서 오른쪽으로 위치변화가 일어나면 +변위, 파동 진행의 반대 방향으로 위치 변화가 일어나면 -변위로 약속하여 그림을 그리면 아래와 같이 Sine파형으로 표현이 가능하다.
파동방정식의 해를 구하면 파동을 표현하는 Sine파형을 구할 수 있다. 축으로 이동하는 소리의 음압(Sound pressure)에 대한 파동방정식은 다음과 같이 표현된다. 여기서
는 음압,
는 공기 밀도,
는 음속이다.
,
편미분 파동방정식의 해가형태가 되는데 앞의 항은 왼쪽에서 오른쪽으로 진행하는 음파를 나타내고, 뒤의 항은 오른쪽에서 왼쪽으로 진행하는 음파를 나타낸다. 오른쪽으로 진행하는 소리파동만을 고려하여 위 미분방정식을 풀되 cosine함수와 sine함수가 위상만 다를 뿐 동일 함수임을 고려하여 정리하면 다음과 같이 sine 파형이 된다.
여기서 를 각진동수(Angular frequency)
로 놓고,
는 파수(Wave number) k로 놓고,
를 활용하면 다음과 같이 음압에 대한 해가 최종 정리된다.
그러므로 종파인 소리파동을 Sine 파형으로 표현할 수 있음을 보여준다. 여기서는 소리의 음압을 기준으로 소리를 표현했으나 매질입자의 변위나 속도로도 음압과 동일한 형식의 사인함수로 표현할 수 있다. 위상만 달라질 뿐이다. 여기서 (wt-kx)를 수학에서는 Argument라 하고 파동에서는 위상(Phase)이라 한다.
sin(wt - kx)에 대하여 좀 더 수학적의미를 음미해 본다. 물체나 음원이나 매질이 제자리에서 진동하면 일차원 공간좌표는 상수가 되고, 오로지 시간함수로만 변위나 진동속도가 표현될 수 있다. 그러므로 진동에 대한 변위는 sin(wt)가 되는 것이다. 그러나 파동은 이들 변위나 속도의 진동이 공간으로 전파해 가는 것이다. 그러므로 sin(wt)를 x축의 양의 방향으로 kx 이동한 모양은 sin(wt - kx) 가 되고, 왼쪽 즉, 음의 방향으로 kx 이동한 파동은 sin(wt + kx)가 되는 것이다. 다시말해 진동이 공간으로 전파하는 파동인 소리는 진동파형을 공간으로 이동하는 것으로 표현할 수 있다는 것이다. 그래프의 이동과 같다.
지금까지 살펴본 바로서 소리는 종파이지만 횡파적 표현이 가능하며, 주파수, 주기, 파장, 진폭, 위상 등의 용어로 표현됨을 알 수 있다. 이는 횡파나 종파나 모두 동일한 수학적 형식의 파동방정식으로 표현될 수 있음을 의미한다.
*(여기서 물결파(Water wave)를 횡파라고 간주하고 예로 사용했지만 실재로 물결파는 횡파가 아니다. 횡파와 유사할 뿐이며, 바닥과 물과의 점성마찰을 무시할 수 없다. 또, 물결파는 중력에 의한 것과 표면장력에 의한 두 부류의 파동이 있다.)
--------------------- by Dajaehun
'소리강의' 카테고리의 다른 글
| 소리파동 방정식(일차원) (5) | 2014.03.24 |
|---|---|
| 소리의 속도(고체) (2) | 2013.07.02 |
| 소리의 속도(액체) (0) | 2013.05.29 |
| 소리의 속도(기체) (0) | 2013.02.22 |
| 단진동 이야기 (0) | 2013.01.01 |





